Prerequisites: Some high school math. A small amount of Calculus and notation often learned in Calculus will be used, but it can be skipped over without losing intuition about the ideas talked about. Knowing the rules of Texas Holdem would be more helpful for this post than Calculus.

How About Some Math I Can Apply?

If you read my last post, you may have walked away from it with the same feelings you had decades ago after math class, “How is counting the ways you can paint a cube at all useful or exciting to my life? Thats a pretty fair point. In my humble opinion, the solution to the problem was more interesting than the one it solved. But the idea of groups isn’t the most applicable mathematical concept to everyday life. Today’s post will prove to be vastly different in this regard.

I won’t be tackling a specific problem today, but discussing and showing examples of one of my favorite topics in applied mathematics: expected value. When people question how mathematics can be used in their lives, I see no better topic than expected value. In fact, understanding expected value can only increase your quality of life. More on this claim to come!

So, What is Expected Value Anyway?

Initially, I planned on using our intuition to arrive at the mathematical definition of expected value, but it would be easier to give the definition with all its mathematical terms and aid it immediately with an example.

Expected value, which I’ll label $E(X)$, is the weighted average of all possible values of a random variable $X$. For discrete random variables, this can be written as $\mathrm{E}(X)=x_1p_1+x_2p_2+...+x_np_n=\sum_{i=1}^{n} x_i p_i$ where the $x$’s are the possible outcomes of the random variable $X$, and the $p$’s are the probability of each outcome.

Okay, I used some fancy math notation and introduced some things that aren’t clearly defined, like random variable. But instead of giving further explanation to this, I’m going to apply this definition to a simple problem, and most of the confusion will subside now.

Let’s Roll a Die

What is the expected value of a dice roll? In other words, what is the average value of rolling a die? Let’s assume we have a fair die, where each side is as likely to appear as any other side.

Our goal is to figure out what the $x$’s are and what the $p$’s are, and then we can plug this in to find the expected value of a roll of dice.

Before we dive right into that, let me introduce the concept of a random variable. What’s annoying about the term “random variable” is that a random variable is actually a function that maps the possible events to a number. In the case of our dice roll, our random variable is the die’s value on a dice roll.

This means that the $x$’s are all the possible rolls of a die, just the numbers 1 through 6.

For the $p$’s, we need to know the probability of each outcome. Because each side is equally as likely to be rolled, all the $p$’s are the same probability, specifically $p=\frac{1}{6}$. Now, we can plug in the $x$’s and the $p$’s to get the expected value, which is $E(X)=1\cdot\frac{1}{6}+2\cdot\frac{1}{6}+3\cdot\frac{1}{6}+4\cdot\frac{1}{6}5\cdot\frac{1}{6}+6\cdot\frac{1}{6}=3.5$ Obviously, you can’t roll a $3.5$ on a standard die. It’s best to think of expected value as a weighted average, where the weight of each value is the probability of that value occurring. What this means is that if we roll a bunch of times (like A LOT of times), we anticipate the average number of the dice roll is 3.5.

What’s powerful about this is that we can find some meaning through randomness. We can apply this concept to help inform our decision-making.

How to Win at Poker

Okay, I’ve clickbaited here a little bit. I don’t have the secret formula for how to win at poker and make millions of dollars. If I do come across this, I’ll make sure to post it on the best website in the world, scotteinsidler.com.

I can say that expected value can be applied to poker to help us learn how to play poker.

Note: Just a disclaimer, I’m going to talk specifically about Texas hold’em.

Why Other Casino Games Suck

Poker is a game you find at a casino, but it’s different from most casino games. Most other casino games involve the casino goers and the casino. When we play these games, we bet on certain outcomes of spinning a wheel, rolling a die, or comparing sets of cards. If you win, the casino matches your bet, and you win what you initially bet, and if you lose, you lose your bet. Let’s say that the amount you can win or lose is $X$, a random variable we can measure in dollars. Then, we can say that $E(X)= \textit{Expected value of the amount we win or lose}$ If we place a bet that is $$x$, for most games, we can assume that we either win $x$ dollars or lose $x$ dollars (losing $x$ dollars is the same as winning $-x$ dollars). With this, we can roughly write out some expected value for a game where we either win or lose a bet against the house as $E(X)=p\cdot x-q\cdot x$ where $p$ is the probability of winning and $q$ is the probability of losing. For example, if you went to Scott’s Fair & Fun Casino and played a game where you bet on fair coin tosses, where you have $1/2$ chance of winning or losing, $p=q=\frac{1}{2}$. This means that the expected value of the coin toss game is $E(X)=\frac{1}{2}x-\frac{1}{2}x=0$ A game where the $E(X)=$ is a fair game. However, most casino games aren’t so fair. Casino games are designed for the odds to be ever so slightly in favor of the casino. Even if every bet is equally matched, the casino games are designed such that $q>p$, so $E(X) < 0$. This means that you lose money on average the more you play!

Poker Is Different, I Swear!

In poker, the expected value is slightly more complicated. Firstly, you usually play more than just one person. But more importantly, all poker rules apply equally to all players. And any of the players can win all the money on the table.

If everything is equal for all players, does that mean that poker is just like the coin toss game at the most generous casino in the world, Scott’s Fair & Fun Casino and has an expected value of zero? Not really. The decisions you make playing poker - folding, betting, checking, raising, and calling - all have different outcomes in the long run. And you are up against opponents who are all trying to make the best decisions given the cards on the board and the two cards in their hand.

I could go into detail about the game theory of poker and how expected value is calculated in Texas Holdem theoretically and in practice, but that could be its own series of posts (which I might do eventually). What’s important to realize is that if you make better decisions than your opponents, we imagine $E(X) > 0$ for you. If you make worse decisions than your opponents, we would imagine that $E(X) < 0$ (Here, our random variable $X$ will represent the amount we win or lose given our actions playing. We won’t be rigorously calculating $E(X)$, so just think about the expected value of what we win over our poker career).

Remember that $E(X)$ here *is different from how much money we have won or lost playing poker. In fact, if $E(X) > 0$, you still could have lost money in the totality of your poker career. This is really what it means to be unlucky or lucky in poker. We intuitively know this when a player goes all in, and bets their whole stack of chips, a player calls his bet with a losing hand, and the last card comes out to make the losing hand now a winning hand. The player who went all in may have decided that, on average, they would have won money, but in this case, they lost a lot.

All of this means it is possible to be a winning player in poker. How you do this is to maximize your expected value of winnings or at least have the expected value of winnings be positive.

How Do Poker Players Use Expected Value?

Today, Poker players can now access poker solvers that can calculate the game theory optimal (GTO) strategy, or at least an excellent approximation. GTO strategy means that every decision you make maximizes your expected profit. While humans can’t play GTO poker due to the immense game state and assumptions players have to make about other players, a studious poker player can use a solver to make sure they are making decisions that optimize their profit over time.

Let’s take a look at an example with a solver to see how expected value comes into play!

Below is a screenshot of a poker solver for a particular hand. Poker solvers usually are for situations where two players are against each other, so we have player 1 and player 2 as different players in our solvers. At the top, we have the game decision tree. This shows the actions taken, the current possible decisions, and when new cards appear on the board. For poker solvers to be able to solve a situation, we have to set a minimal number of specific bet sizes. This helps to make the game tree a reasonable size. Otherwise, we would have to wait lifetimes before studying a hand!

We are also given a table of all the hands, sorted by highest to lowest equity (let’s not get into that concept now, for another post), along with “EV,” or our good ole friend, expected value!

It’s also important to note that the solver is used for all the betting after seeing the first three cards. On the left, we can see the board: the King of Hearts, ten of Hearts, and Eight of Spades. Allow me to abbreviate this as KhTh8s, where the “h” represents “hearts” and the s is “spades” (“d” is for “diamonds” and “c” is clubs, of course).

The last important thing to note is that the big grid in the middle shows all the hands you would be left with (that you haven’t folded at some point, according to the solver). They are colored by the actions you should most likely take.

One way I study with solvers is to take particular spots I encounter and review whether my decisions cost me expected value. For example, let’s say I’m player one, and I have Qc8c in my hand, and we play out the hand according to the image of the solver above. In other words, KhTh8s6s5c is on the board, and it is my turn to bet. Here, we restrict ourselves to three possible decisions: a huge all-in bet, a small bet, or a check. It’s also good to note that the currently has $90 in it in this scenario, and we have $449 in our own stack of chips.

If we look at the row of the table for Qc8c, we get what’s shown below.

We can see that our EV (or expected value) overall for our hand is $26.81. Considering the pot being $90, this doesn’t look too good for our hand, but it certainly could be worse. We have a pair of eights, which is beaten by a lot but can beat some worthless hands.

The colorful numbers next to the expected value are the expected value of each decision; the dark blue number is the expected value of a big bet, the pink number is the expected value of a small bet. The green number is the expected value of a check. As we can see, making a big bet has a negative expected value of $-53.07. It would be a terrible decision to go all in with eights here!

But should we bet at all? Even a little bit? The expected value of a small bet is $25.31, while just checking has an expected value of $26.81. While this is a slight difference, these decisions compound over time. That’s why the solver decision is purely checked here and never betting, and the expected value of Qc8c at this point in the hand is the same as checking.

That’s enough about poker! We can see how expected value is helpful for poker, but how does it apply to the diamond?

How to Win at Baseball

One of my favorite books of all time (the movie is pretty good, too), Moneyball: The Art of Winning an Unfair Game by Michael Lewis, documents the start of the data revolution in baseball. More specifically, Michael Lewis follows general manager Billy Beane of the Oakland A’s during the 2002 season. Billy Beane and the Oakland A’s were trying to do something no other baseball team had attempted: use a data driven approach to try to win baseball games.

I highly recommend reading the book for yourself. Especially if you appreciate sports or data science.

Some of the conclusions that Billy Beane and the management of the A’s came to are widely accepted today. However, they certainly weren’t twenty years ago. For example, they found that how often you get on base, or your on-base percentage, was way more important than how much you hit the ball or your batting average.

But central to their findings was the use of expected value to determine what actions lead to more runs and which players lead to more runs than their salary allows.

Using Expected Value In Baseball

Ultimately, suppose you are on a professional baseball team. In that case, you want to do everything you can to maximize the points you get during a season. While you can’t control how your opponents play, you, as a team, can put yourself in the best position to win. In other words, you want to maximize the expected number of runs during a season and minimize the number of expected runs against you.

In fact, baseball statisticians have gone through all the available play-by-play data to develop a simple matrix that captures the expected value of all the possible configurations of runners on base and the number of outs called the *run expectancy matrix. This matrix tells us how many runs are expected to be scored from this point up until the end of the inning. Below is the run expectancy matrix that I found from here.

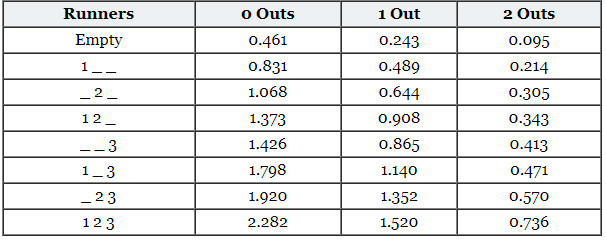
Here, each row is a different configuration of runners. For example, “1_ _” is a runner on first, and “ _ 2 _” means there is a runner on second, etc. We can take the difference of two game states to determine whether an action won our team or lost our team’s expected runs.

For example, suppose there is one out, and we have runners on first and second. When we step up to the plate, our team’s expected runs are 0.908, according to the matrix. If I ground out so that there are two outs and runners on first and second, our expected runs shoot down to 0.343. This means that the expected runs of the ground out is $0.343-0.908=-0.565$ expected runs. Not Good!

However, if, instead, we hit a single so that the bases are loaded, our expected value now shoots up to 1.520, making the expected runs for the single $1.520-0.908=0.612$

There are many other uses for expected value in baseball, and the A’s utilized expected value for evaluating the players’ value and how to play the game itself. But enough about baseball already!

How to Win At Life

Okay, this is the last clickbait in this post, I promise. But expected value can at least help you fight off your human instincts when these instincts cause you to make decisions antithetical to your goals!

Take More Risks, My Friends!

Veritasium made a video asking people on the street if they would take a bet that is identical to the bet I posed earlier made by Scott’s Fair & Fun Casino. He asked people to bet on a coin flip. If they win, they get $10 (I think it was some other currency I couldn’t recognize, but the specific currency is irrelevant to the point). If they lose, they lose $10. As we discussed before, and as Veritasium discusses, this is a fair bet. That means you would be breaking even taking this bet. No one took the bet.

He then asked people if instead of winning $10, you win $15 instead. Still, no one took it.

With our knowledge of expected value, we can see that the expected value of this bet for us, assuming a fair coin, is $\frac{1}{2}\cdot $15 -\frac{1}{2}\cdot $10=$2.50$ so we should take this bet because we expect to win $2.50 on average.

He kept increasing the winnings, but people still refused. The feeling of losing money was more present in their minds than the chance of winning money. This is part of our own psychology. But with our knowledge of expected value, we can find when risks are worth taking!

Let’s Get Philosophical

What is to come is my opinion. I’m not a philosopher. But I believe we all have our own values, and everyone can construct their own value functions of how much they value specific outcomes over others. This could be choosing a job to work, picking plans for the evening, or any other decision we have put in front of us. If we know how likely things are to occur and the value they give us, we can construct the expected value of every decision we make. Our goal in life is to maximize the expected value of our choices according to our value functions.

What is your value function? Does it change over time? Honestly, I’m not sure. However, applying expected value to your life helps you understand how to properly weigh decisions. Yes, applying to that job you want is almost pointless because you don’t think you have a good chance. But is the payoff of getting the job valuable enough to you that you might as well try?

Conclusion

I said more than I wanted to about expected value. Still, I hope I’ve shown how useful of an idea it is in several contexts. This post also made me realize that I should write more posts in the future on the mathematics involved in poker. If that’s something people want, I’ll do that sooner rather than later.

I also hope it’s clear that I don’t expect you to be able to calculate the expected value of various random variables from this post but rather show how a concept as robust as the expected value can be applied to many scenarios and can be applied to your own lives. I might revisit this topic to give it more justice in the future, but for now, go off and buy some lottery tickets if the probabilities are correct!